At this stage, with the initial conditions set, all of the
coefficients ![]() are determined (
are determined (![]() ), so it is a
straightforward matter to evolve the magnetic field by using equation
(23), for each point
), so it is a
straightforward matter to evolve the magnetic field by using equation
(23), for each point ![]() desired.
desired.
I chose a grid of
![]() points in the
points in the ![]() plane, which
covered 0-20 light seconds in each direction. The equation was
evolved for 40 seconds, which is long enough time for all waves to
propagate across the grid. The initial condition is shown in this
density plot. It shows a concentration of magnetic flux near the ring
plane, which
covered 0-20 light seconds in each direction. The equation was
evolved for 40 seconds, which is long enough time for all waves to
propagate across the grid. The initial condition is shown in this
density plot. It shows a concentration of magnetic flux near the ring
![]() .
.
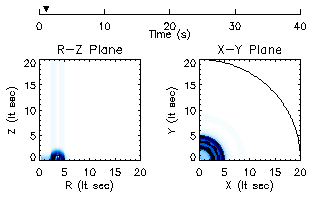
(The box on the left shows the initial position of the toroid, as does the dashed ring on the right. The outer ring is the outer extent of the computation.)
After about 5 seconds of evolution, the magnetic field has expanded
from its initial configuration, and has begun to interact near the
origin. This is probably constructive interference due to the wave
converging at the ![]() -axis, similar to focusing of light.
-axis, similar to focusing of light.
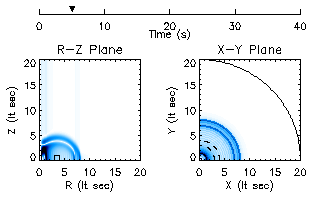
Finally, after 25 seconds of evolution, the waves have moved well away from the original position of the toroid, and show no signs of returning. Indeed, after 30 seconds, the waves have completely left the grid.
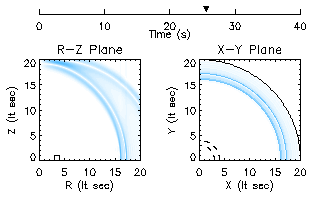
Finally, CLICK HERE
FOR
THE FULL MOVIE, which is an animated GIF of about 400 kilobytes. It
shows the time evolution in both ![]() and
and ![]() planes, up to to 40
seconds. The magnetic field is always in the azimuthal direction
(
planes, up to to 40
seconds. The magnetic field is always in the azimuthal direction
(![]() ), and is of arbitrary strength. Only the magnitude is
shown, not the direction. A wave is seen to form, which indeed
propagates outward at the speed of light. The final magnetic field
intensity at the original position of the flux loop is less than
0.01% of the starting value.
), and is of arbitrary strength. Only the magnitude is
shown, not the direction. A wave is seen to form, which indeed
propagates outward at the speed of light. The final magnetic field
intensity at the original position of the flux loop is less than
0.01% of the starting value.