| (26) |
Please note that while I haven't explicitly solved for the electric
field, there must be an electric field because Maxwell's equations
require it when there is a time-varying magnetic field. The wave
equation (5) implicitly involves the electric field
equations as I verified in equations (6)-(7).
Indeed, the electric field can be formed explicitly using Ampere's Law
from Maxwell's equations,
| (26) |
| (27) |
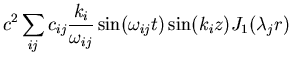 |
(28) | ||
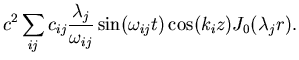 |
(29) |
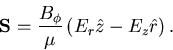 |
(30) |
It can be shown that this field configuration is effectively poloidal near an antinode in the magnetic field strength. Near such
an antinode, the fields for a single eigenmode can be expanded in
terms of a small vector displacement from the center,
![]() . The results are reasonably straightforward, and
give a Poynting flux of
. The results are reasonably straightforward, and
give a Poynting flux of
| (31) |
The flux is alternately directed radially outward and then inward. One might say that that the total energy content in a single peak is conserved because the influx cancels the outflux, and this is strictly true! Because an eigenmode extends infinitely throughout space, and does not decay with time, it must be the case that the total energy in a peak is conserved over one cycle.
However, I have already shown that a flux loop cannot be expressed as a single eigenmode, so the above equation is not valid for the flux loop solution. Also, the Poynting flux is not additive, which means that we cannot simply add the Poynting fluxes due to each eigenmode separately. Rather, we must first add all the component fields together as described above, and then compute the Poynting flux.
I have done this, and here are a few examples. All of the plots show
the Poynting flux along the radial axis where ![]() . An
inward-pointing flux is coded as red, and an outward-pointing flux is
coded as blue. Shortly after the start, there are an inward- and
outward-moving set of fluxes originating from the original toroid.
. An
inward-pointing flux is coded as red, and an outward-pointing flux is
coded as blue. Shortly after the start, there are an inward- and
outward-moving set of fluxes originating from the original toroid.
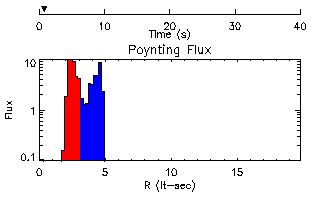
At a later time the waves have continued to travel. The outward-moving wave proceeds unimpeded, while the inward-moving wave interacts at the origin.
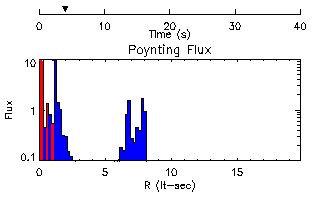
At late times, both waves are moving outward and continue indefinitely beyond the range of computation.
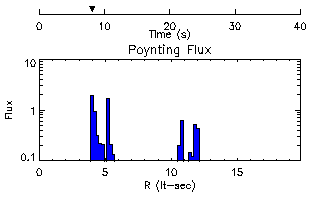
Finally, an animated GIF movie (110 kilobytes) shows the full time evolution of the Poynting flux.