A professor keeps improving his thesis for the rest of his career.
This is a collection of theory projects addressing long-standing questions in physics. The following essays and papers are meant to inject fresh thoughts into problems that have resisted conventional thinking for a long time. Some of these ideas may seem far-fetched. Critique and suggestions are welcomed (e-mail: fhimpsel@wisc.edu).
Analyzing the forces that act on the electron might also shed light onto the strength of the electromagnetic interaction. It is quantified by the electromagnetic coupling constant (the square of the elementary charge). This is the famous fine structure constant alpha, discovered by Sommerfeld in 1916. Feynman once wrote that all good theoretical physicists put the value of alpha up on their wall and worry about it. Balancing electromagnetic against non-electromagnetic forces might determine alpha and thereby solve both of these century-old problems in one stroke.
The total energy balance is often explained qualitatively in terms of forces by saying that the electrostatic attraction is balaced by the Pauli repulsion, i.e., the quantum-mechanical repulsion due to Pauli's exclusion principle. To express this statement mathematically, one can use the Lagrangian formalism which serves as the basis of particle theory. Technically, the force density is obtained from the divergence of Maxwell's stress tensor. Applying this formalism to the hydrogen atom, I found that the electrostatic attraction exactly balances the kinetic repulsion at every point inside the H atom (see the two links below).
At a first glance, such a local force density balance might seem incompatible with the uncertainty relation, which implies that one cannot localize an electron exactly without applying an infinitely large momentum. But that holds only for a single experiment. If the experiment is repeated many times with many momenta, one obtains a probability density for the location of the electron inside the hydrogen atom. This can be accomplished by repeated scattering experiments. Such experiments have been used to determine the charge distribution inside the proton (its "form factor").
Force Density Balance inside the Hydrogen Atom, arXiv:1511.07782 [physics.atom-ph]
Hyperfine Wave Functions and Force Densities for the Hydrogen Atom, arXiv:1702.05844 [physics.atom-ph]
A prototypical example is the vacuum polarization, a faint halo of opposite charges surrounding every charged particle. That creates a situation reminiscent of the H atom, where the electrostatic attraction needs to be balanced by the repulsion from squeezing. But the vacuum polarization charges are squeezed much harder, down to the reduced Compton wavelength. That is a factor of alpha smaller than the Bohr radius of the H atom (alpha ~ 1/137).
It turns out that the force balance remains intact for the vacuum polarisation surrounding an electron. One can show that each spherically-symmetric shell of vacuum electrons and positrons is balanced. The subsequent sum over the infinite number of such shells in the Dirac sea is tricky, but can be performed by adapting a method from calculations of the vacuum polarization itself. Since every charged particle is surrounded by the same electron/positron vacuum polarization at large distances, this force balance is common to all charged particles.

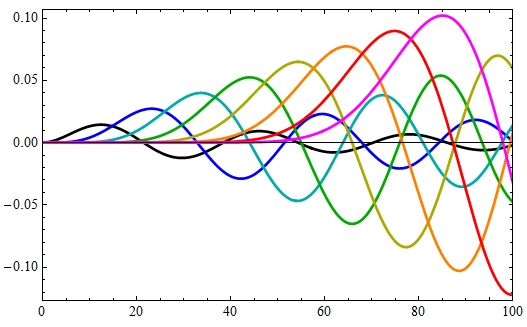
The figure illustrates the summation over the charge densities of all electrons and positrons in the Dirac sea surrounding a positive point charge. These are spherical wave solutions of the Dirac equation in the Coulomb potential of the reference electron. They are characterized by two quantum numbers, the radial momentum (plotted along the x-axis) and the angular momentum (which increases in steps of 1 from black to magenta). The distance from the point charge is fixed at 1/10 of the reduced Compton wavelength in this plot. Notice the many near-cancellations which complicate the calculation.
The Stability of the Vacuum Polarization Surrounding a Charged Particle, arXiv:1512.08257 [quant-ph]
This argument does not apply to the H atom, where the Coulomb interaction occurs between a single electron and the proton. But it applies to any situation involving more than one electron, such as the interaction of an electron with the Dirac sea. In addition to the Coulomb interaction discussed in the previous section one has to include the exchange interaction.
These arguments can be quantified by the Hartree-Fock method which includes separate terms for the Coulomb and the exchange interaction. The self-Coulomb term is canceled automatically by the self-exchange term.
To illustrate this concept it is useful to return to the Fermi sea, the analog of the Dirac sea in metals. The exclusion principle generates a depletion of electrons in the Fermi sea near a specified reference electron. This so-called exchange hole exactly compensates the negative charge of the reference electron and thereby strongly reduces its Coulomb interaction with the remaining Fermi sea.
This well-studied phenomenon suggests the existence of an exchange hole not only in the Fermi sea, but also in the Dirac sea. Such an object can be defined, as shown in the figure and the reference below. The exchange hole in the Dirac sea extends over the reduced Compton wavelength, which is 100-1000 times smaller than typical exchange holes in the Fermi sea.
The size difference can be traced to different cutoffs in a sum over all pairs. The Fermi sea contains electrons with wavelengths ranging from infinity down to the Fermi wavelength (which depends on the electron density). The Dirac sea, on the other hand, contains electrons and positrons with all possible wavelengths (which leads to infinite densities of electrons and positrons). The resulting infinities cancel out between electrons and positrons and leave a finite result for the size of the exchange hole. It is comparable to the reduced Compton wavelength, the only available length scale.
This scheme can be extended to multiple exchange interactions using the Hartree-Fock method. Including double-exchange leads to an exchange hole surrounded by an exchange electron (the "exchange hole of the exchange hole"). That solves a problem with charge conservation, because the reference electron is now surrounded by a neutral electron-hole pair, the exchange exciton.
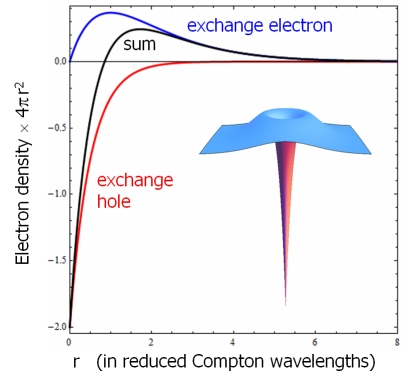
Above: Radial electron densities of the exchange hole, the exchange electron, and their sum (also shown in 3D as inset). The switch from hole to electron character occurs near the reduced Compton wavelength.
After figuring out the exchange interaction in the Dirac sea, one can return to the original goal of balancing the forces acting on the reference electron, the exchange hole, and the exchange electron. This object resembles the negative ion of positronium, which has been investigated both theoretically and experimentally.
The Exchange Hole in the Dirac Sea, arXiv:1701.08080 [quant-ph]
The Higgs boson, the Higgs potential, and the Brout-Englert-Higgs mechanism of symmetry breaking are central to the standard model of particle physics (therefore a well-deserved Physics Nobel Prize in 2013). This mechanism explains how our universe is able to generate masses for fundamental particles by breaking a symmetry in the laws of physics. (Composite particles, such as the proton, can acquire mass by a different mechanism, where the kinetic energy of their constituents is equivalent to mass according to Einstein.)
But the current standard model of particle physics contains a Higgs boson that blemishes the elegance of the theory. It postulates an ad-hoc potential for the Higgs boson which contains a quadratic term that mimics a mass term, but has the wrong sign (corresponding to an imaginary mass). A fourth-order term is added, even though it is absent for all other fundamental particles. The standard Higgs potential contains two adjustable parameters, one of them being the mass of the Higgs boson. This construct looks rather artificial, which has been a concern to many theorists. As a result, models have been proposed where the Higgs particle is not fundamental, but composed of pairs of fundamental fermions (similar to the electron pairs in superconductors). But such models are outperformed by the standard Higgs potential, which matches the data with the help of adjustable parameters.
My contribution to the extensive search for a better Higgs model is the idea of constructing a Higgs boson from bosons instead of fermions. The fundamental bosons are the gauge bosons, which are related to symmetry. The theory of symmetry groups assigns gauge bosons to a unique group representation (labeled the adjoint). Consequently, the construction of the composite Higgs boson is uniquely determined by symmetry. That lends a certain elegance to this model: The Higgs boson consists of gauge bosons, which in turn originate from symmetry.
Gauge bosons mediate interactions and thereby become an essential part of particle theory. In the standard model, the photon mediates the electromagentic interaction, the W and Z mediate the weak interaction, and the gluons the strong interaction. Each interaction corresponds to a characteristic symmetry. If the symmetry is preserved, the corresponding gauge bosons are massless (such as the photon). If the symmetry is broken, the gauge bosons acquire mass (such as the W and Z). Since the Higgs boson breaks the symmetry of the weak interaction, one might suspect that its mass is related to the W and Z masses.
The standard model and its extensions are unable to explain the Higgs mass. That's why it took so long to find the Higgs boson. It required searching for a narrow Higgs resonance in a wide energy range of ca. 100-1000 GeV. Even after its discovery, the mass of the Higgs boson remains an unexplained parameter.
Why has this Higgs model not been considered previously? It seems to imply a finite "vacuum expectation value" (VEV) for the gauge bosons, which then seems to imply a preferred direction in vacuum. To appreciate that, one has to go back to the Brout-Englert-Higgs mechanism of symmetry breaking. The Higgs boson needs to acquire a finite VEV to break the symmetry of the weak interaction. Viewing the Higgs particle as a wave, its VEV corresponds to a constant, finite amplitude around which it oscillates (instead of symmetrically around zero). This concept raises concerns, because gauge bosons are vector particles. Each of them points in a certain direction. The VEV of a vector particle would define a preferred direction in space. Consequently, the rotational symmetry of the vacuum would be broken.
But there is a loophole. One can choose an individual direction for the expectation value (EV) of each virtual gauge boson in the vacuum of quantum field theory. Rotational symmetry of the vacuum is restored by averaging over the EVs of all virtual gauge bosons. They compensate each other and lead to a vanishing VEV. The same argument holds for the the momentum vectors of virtual particles in vacuum.
Scalars, such as the Higgs boson, do not have a preferred direction and thus can have a non-zero VEV. This is also true for the the scalar product of a gauge boson with itself, i.e., a pair of gauge bosons. This concept is analogous to that used in Higgs models using fermion pairs. Such considerations suggest using scalar WW and ZZ pairs to represent a Higgs boson (actually a pair of Higgs bosons). In order to satisfy the gauge symmetry of the weak interaction, the gauge boson pairs are arranged in the singlet configuration. The remaining proportionality constant is determined by setting the mass Lagrangians of the Higgs and gauge bosons equal to each other.
The resulting relation between gauge and Higgs bosons immediately relates the mass of the Higgs boson to that of the W gauge boson. Furthermore, the Higgs mass becomes simply half of the Higgs VEV, which can be obtained directly from Fermi's coupling constant GF. The resulting value matches the observed Higgs mass within 2% . That is comparable to the accuracy of the leading-order approximation used in this work.
One might ask, how the W and Z gauge bosons develop finite VEVs without an artificial Higgs-like potential. It turns out that they interact with each other and even with themselves, due to the "non-abelian" symmetry of the weak interaction. Such self-interactions lead to quadratic and quartic terms resembling the two terms of the standard Higgs potential. They can be calculated from a collection of Feynman diagrams. Those are shown in the overview talk above and the references below. While the evaluation of the diagrams is too complex for a non-specialist, it remains at the one-loop level which can easily be handled by today's codes. If the resulting gauge boson potential breaks the weak symmetry, the proposed model would become self-consistent and yield a new standard model with fewer adjustable parameters. That would also be one step further in the ancient quest to disect matter into ever smaller pieces, until they cannot be divided any more.
To observe pairing of Higgs bosons (and gauge bosons) will require energies near the 250 GeV threshold. This energy also matches the Higgs VEV of 246 GeV (within the leading-order approximation adopted here). It would be particularly interesting to look for resonances in elastic gauge boson scattering, caused by an intermediate Higgs pair. Combining precision measurements of the Higgs mass with calculations beyond the leading order should enable a critical test against other models for the Higgs boson.
To get started without elaborate calculations or experiments, one can construct an empirical gauge boson potential analogous to the standard Higgs potential. This involves adjustable parameters which are to be matched to observables (for example the masses of the gauge bosons and Fermi's coupling constant). The first publication below shows that this is indeed possible. The resulting potential can then be plotted as a function of WW and ZZ pairs, as shown in the figure. There are two topologically distinct cases, with a minimum occuring either along a line or at a point.
The second publication below reveals an interesting connection to Yang-Mills theories, a general class of gauge theories. They play a dominant role in the standard model and its extensions. The simplest example is based on the SU(2) gauge symmetry of the weak interaction. Among the fundamental questions are the mechanism of symmetry breaking, the resulting generation of mass, and the very existence of Yang-Mills theories (by rigorous mathematical standards). One of the seven Millenium Prizes of the Clay Mathematics Institute is dedicated to these questions.
The last two papers address the required modifications in the codes evaluating the standard model. They are summarized by three simple rules. After including interactions with fermions, this composite Higgs model covers the complete particle content of the standard model.
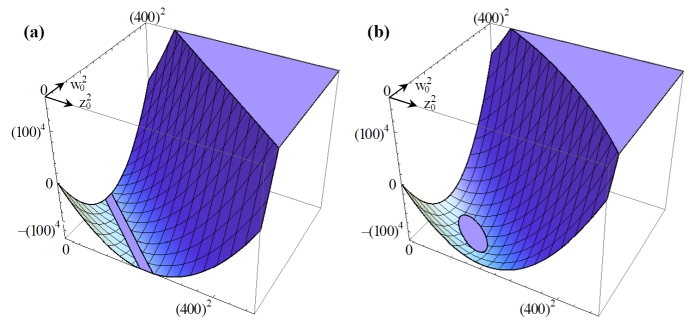
Above: The two possible topologies for the potential of the composite Higgs boson, plotted in terms of WW and ZZ pairs
(in units of GeV). Such potentials replace the traditional
Higgs potential. They can be calculated from the gauge boson
self-interactions.
A Higgs Boson Composed of Gauge Bosons,
arXiv:1502.06438 [hep-ph]
Dynamical Symmetry Breaking by SU(2) Gauge Bosons,
arXiv:1801.04604 [hep-ph] ,
Updated Version
Work in Progress:
Fermion Masses and Couplings in a Composite Higgs Model
Boson Couplings in a Composite Higgs Model
This project started with the notion that any realistic theory of the four fundamental interactions has inherently nonlinear character. When fields/particles interact with each other, they violate the superposition principle by generating scattered waves/particles. Most notably, Einstein's equations for gravity in curved space-time are highly nonlinear. Nevertheless, classical and quantum fields are typically expanded into non-interacting sinusoidal waves when describing scattering. Would it be possible to develop an expansion into a more general class of interacting waves? What are the criteria for such waves to satisfy basic priciples of physics?
Anharmonic waves might become useful to describe multiphoton effects in free electron lasers, the strong interaction in nuclei, and the emission of gravity waves from black holes.
In laser physics and acoustics, sinusoidal waves are characteristic of linear media. Nonlinear media generate harmonics. These are described by a Fourier series of sinusoidal waves which contain integer multiples of a fundamental frequency. It turns out that three simple constraints make anharmonic waves compatible with relativistic field theory and quantum physics. Some familiar concepts have to be abandoned, such as the superposition principle (of course), orthogonality, and the existence of single-particle eigenstates.
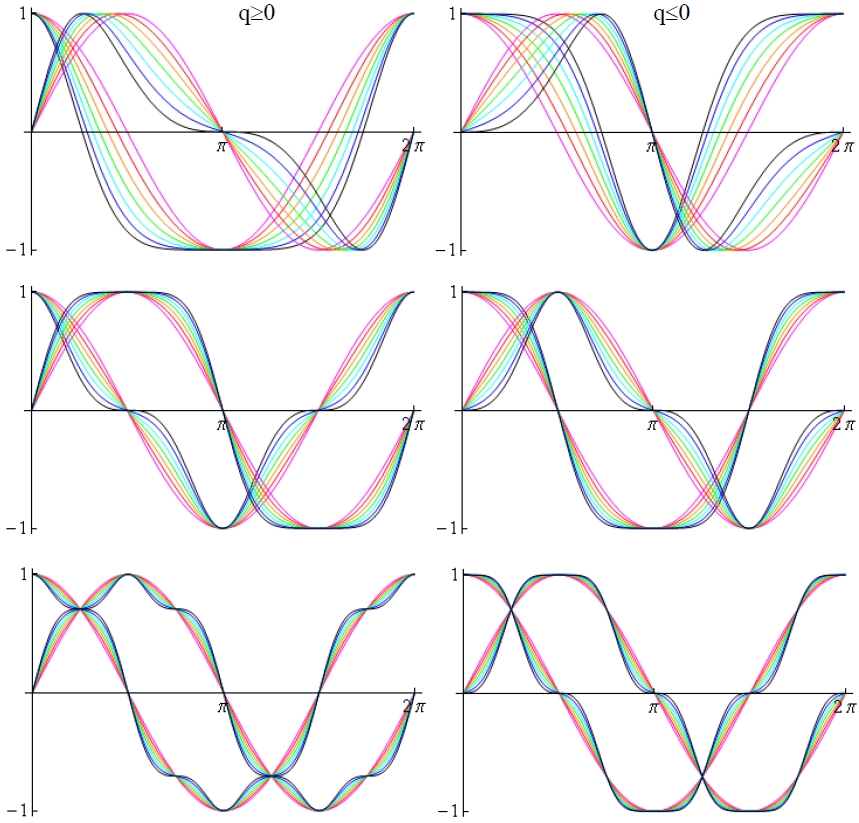
The figure shows three generic symmetries of anharmonic waves that satisfy the ground rules of relativity and quantum physics. The parameter q represents the strength of the anharmonicity, increasing from zero (red) to the maximum (black). The two sets of curves in each panel are the anharmonic generalizations of sine and cosine. In all cases the familiar relation ( sin2x + cos2x ) = 1 remains valid. This is achieved by a periodic phase modulation of sine and cosine. For the waves with lowest symmetry (top row) either the sine or cosine develops a non-zero average. That corresponds to a non-zero vacuum expectation value in quantum field theory (see the section about the Higgs boson above).
Anharmonic Waves in Field Theory,
arXiv:1108.1736 [hep-th]
Quantum Electrodynamics with Anharmonic Waves,
arXiv:1112.6216 [hep-th]